Posts

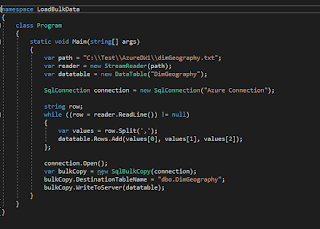
Modern Day Data Warehousing

Image
With ever growing data volumes and the need to necessitate a faster approach into making rapid decisions on your data sets, numerous technologies have emerged in the past 5 years trying to blend  the transactional pipelines, the data storage and the analytics together. The modern day data warehouse consists of dumping the data into more of a containerized approach catering away from the traditional star and snowflake schemas of the past. Not that these data warehouse schemas have been extinguished but more in tune with rapid assembly and disassembly of data in containers. The core aspect is to whether to de-containerize  the data as soon as it comes into our storage layer or go about doing it in an adhoc fashion with your containers being pipelined further into data virtualization stores, data marts or even just reporting on top of the data brought into the data lake, a virtualized data warehouse, an in memory data mart etc... Almost all modern day architectures have started mo
Post a Comment
Read more

TFS Usage

Image
I was asked a few questions about TFS by a customer a couple of years ago.... I was rummaging through some of my luggage and found the questionairre. Just thought I would answer the questions with this blog post before throwing it away: 1. How would you breakdown TFS Projects? The manner in which TFS projects can be broken down is into identifiable work items with tasks associated to them. 2. Once the Work Item is defined, what are the next steps? The above image does not belong to me but would love to thank the author for the same. Review the requirements that are assigned to the iteration, and define them in more detail. •Create task work items for the work that must be performed to implement and test each requirement. Link the tasks to the requirement work item by using the parent link type. •Set the Original Estimate field of each task. •Divide tasks that have estimates that are longer than a few days. •Compare the estimates with the time that is available for
Post a Comment
Read more

Branding your SharePoint site in a super fast way - Emgage

Branding a SharePoint farm on premise or in O365 is an extremely time absorbing task. Recently found a few tools called emgage prime and emgage turbo which basically gives you customized UX branding solutions to make you get to what you want super fast and super easy....Just used it on a SP2016 farm a few days ago and the results were tremendous. A definite recommendation on the SP side of things.
Post a Comment
Read more

Load Data into Azure DW using C# in an SSIS script task

Image
Now there are a lot of reasons why SSIS needs to be leveraged for loading data into the Azure DW platform. Even though Polybase and Azure Data factory are the core criteria's, here are the templates for the SSIS script task that were leveraged to load data (full and incremental into Azure DW) for a specific customer rather than using the data flow task: SSIS Full Load script : SSIS Incremental Load script : There are a few reasons for this approach and one of them being that the existing package was using a similar structure and one not to be deviated from. The other being that some key logging aspects needed to be handled in a Legacy platform that could not be decommissioned at that time.
4 comments
Read more

Why Azure might overtake AWS in its data services offerings

Image
Compliance Microsoft enterprise cloud services are independently validated through certifications and attestations, as well as third-party audits. In-scope services within the Microsoft Cloud meet key international and industry-specific compliance standards, such as ISO/IEC 27001 and ISO/IEC 27018, FedRAMP, and SOC 1 and SOC 2. They also meet regional and country-specific standards and contractual commitments, including the EU Model Clauses, UK G-Cloud, Singapore MTCS, and Australia CCSL (IRAP). In addition, rigorous third-party audits, such as by the British Standards Institution and Deloitte, validate the adherence of our cloud services to the strict requirements these standards mandate. Security With Security tightly ingrained with its AD offerings, Microsoft currently continues to evolve its security   and data integrity in Azure. Core advantages of Security in Azure are as follows: Tightly integrated with Windows Active Directory Simplified cl
Post a Comment
Read more

Modern Day Messaging Patterns

Its been a few days now and I have been focused on understanding modern day messaging patterns for a problem I am trying to solve. I do know that there are existing server side tools like Active MQ, Rabbit MQ and even WMS that can do the trick and already have pre-defined patterns tested and validated for performance and security but in this case even though I am not trying to reinvent the wheel in terms of creating a new pattern or any of these server side products, I am definitely trying to understand the manner in which these products have been created and if I can actually leverage some of the principles in a server side application I am writing up. For example in modern based web application development, if .Net based, you have patterns like the one's defined here: Microsoft SOA patterns  that do the neat tricks you would need. Man at times I feel I am going at 300 miles an hour without any crash guards: Code reviews, Custom product development, Customer Engagements, Team man
Post a Comment
Read more

Power BI To Embed Or Not To Embed

It is very critical for organizations to work & play with data. Power BI - the reporting solution from Microsoft is literally scorching the market with its rapid pace in usage. On a quick note while interacting with your Power BI report like the following--> This report is accessible by the public. In order to create a more personalized/advanced security reporting structure with Power BI, the Power BI embedded would be the way to go. Create a workspace collection in Azure and then generate the required API keys (two by default - primary and secondary). These API keys will be leveraged by your web application. Once this is done create the pbix solution file in your desktop tool and publish or import the pbix solution to the Azure workspace using powershell/C#/ruby/java etc... Now to interact with the pbix file in your application, you need to leverage the Power BI Embed API's. However there is another approach using Power BI API's instead of the embed API's. The em
2 comments
Read more